Tower of Hanoi

題目

河內塔是一個有三個堆疊（左、中、右）以及 $n$ 個尺寸各異圓盤的遊戲。遊戲一開始，左堆疊會堆滿所有圓盤，圓盤尺寸從上到下遞增。

遊戲目標是透過一系列操作把左堆疊上的所有圓盤移動到右堆疊。每次操作都是將一個堆疊最上方的圓盤放到另一個堆疊的最上方，但不能把尺寸大的圓盤放到尺寸小的圓盤上。

你的任務是找出最少操作次數的解法。

輸入

一個正整數 $n$ 代表圓盤總數量。（$1 \le n \le 16$）

輸出

• 第一行輸出整數 $k$ 代表操作次數。
• 接著輸出 $k$ 行，每行輸出兩個整數 $a$、$b$，代表將一個圓盤從堆疊 $a$ 移動到堆疊 $b$。（堆疊左、中、右分別為 $1$、$2$、$3$）

範例測資

Input :
2

Output :
3
1 2
1 3
2 3

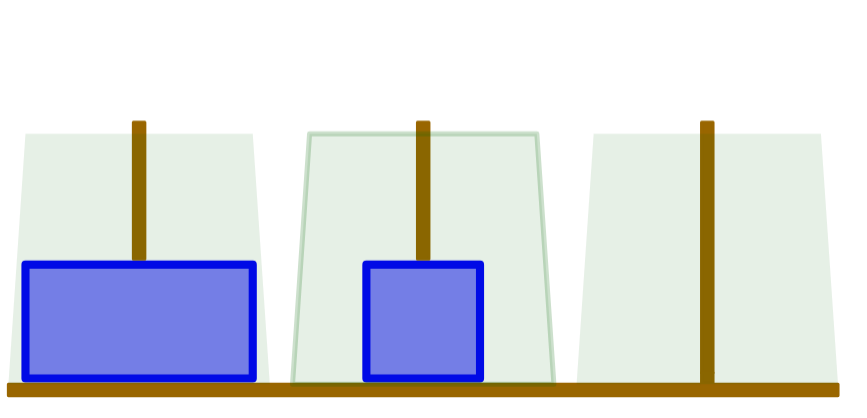
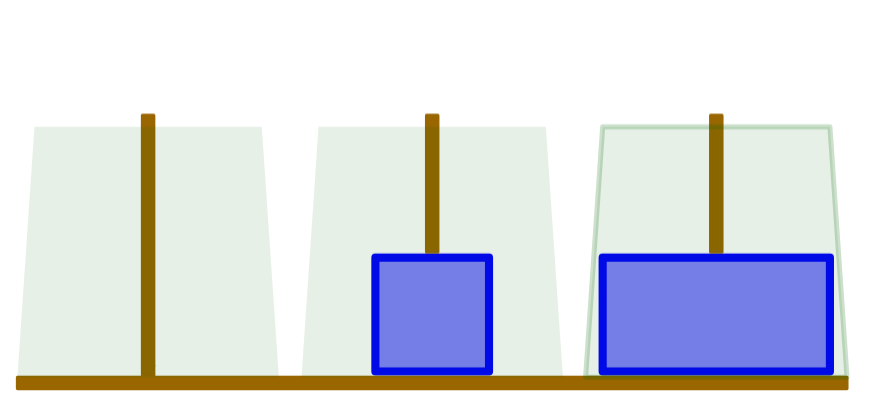
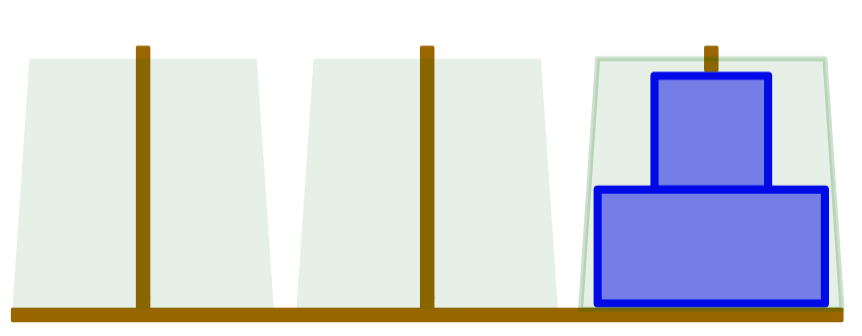
圖源 : https://www.geogebra.org/m/xmAHgGhA

想法

這個遊戲其實並不複雜。因為大圓盤不能放在小圓盤上方，如果要將最大的圓盤從堆疊 $1$ 移動到堆疊 $3$，其他所有圓盤都必須先放在堆疊 $2$ 上才可以。也就是說一個有 $n$ 個圓盤的河內塔一定會分解成下面三大步驟：

1. 把前 $n-1$ 個圓盤從堆疊 $1$ 移動到堆疊 $2$
2. 把最大的圓盤從從堆疊 $1$ 移動到堆疊 $3$
3. 把前 $n-1$ 個圓盤從堆疊 $2$ 移動到堆疊 $3$

我們會發現步驟 1 跟步驟 3 其實也是一個河內塔遊戲，只是圓盤數量變成 $n-1$，而且起點與終點的堆疊不一樣而已。我們可以用遞迴寫出這些步驟，而且因為步驟 2 是必須的，這個解法的操作數一定是最少的。

我們可以用一個變數紀錄操作次數，並在遞迴中慢慢累加，但我們也可以直接用公式求出。令 $H(n)$ 為 $n$ 圓盤河內塔遊戲的最少操作次數，那麼就有 $H(1) = 1$，並且我們可以根據上面的步驟拆解得出遞迴關係式 $H(n) = 1 + 2H(n-1).$ 而這其實就是 $n$ 層滿二元樹的節點數量，也就是說 $H(n) = 2^n - 1.$

範例程式碼

C++ 範例

#include <iostream>
using namespace std;

void hanoi(int n, int from_s, int to_s, int aux_s) {
    if (n == 1) {
        cout << from_s << ' ' << to_s << '\n';
    } else {
        hanoi(n-1, from_s, aux_s, to_s);
        cout << from_s << ' ' << to_s << '\n';
        hanoi(n-1, aux_s, to_s, from_s);
    }
}

int main() {
    int n;
    cin >> n;
    cout << (1 << n) - 1 << '\n';
    hanoi(n, 1, 3, 2);
}