Number Spiral

題目

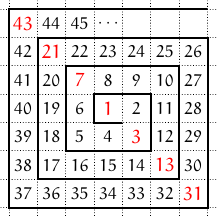
Number spiral 是一個無限大的數字網格，其中左上角的格子數字為 $1$。下圖是 number spiral 的前五層：

你的任務是找出位在第 $y$ 橫列、第 $x$ 直行上的數字 $N(y,x)$。

輸入

• 第一行有一個正整數 $t$ 代表子測資的數量。（$1 \le t \le 10^5$）
• 接下來有 $t$ 行，每行有兩個正整數 $y$ 與 $x$。（$1 \le y, x \le 10^9$）

輸出

輸出 $t$ 行，各自對應一個子測資。 對每個子測資，輸出位在第 $y$ 橫列、第 $x$ 直行上的數字 $N(y,x)$。

範例測資

Input :
3
2 3
1 1
4 2

Output :
8
1
15

直接對照表格的座標後輸出該座標上的數字

想法

首先，我們可以觀察這條對角線（也就是位於第 $i$ 橫列第 $i$ 直行的格子）的規律。

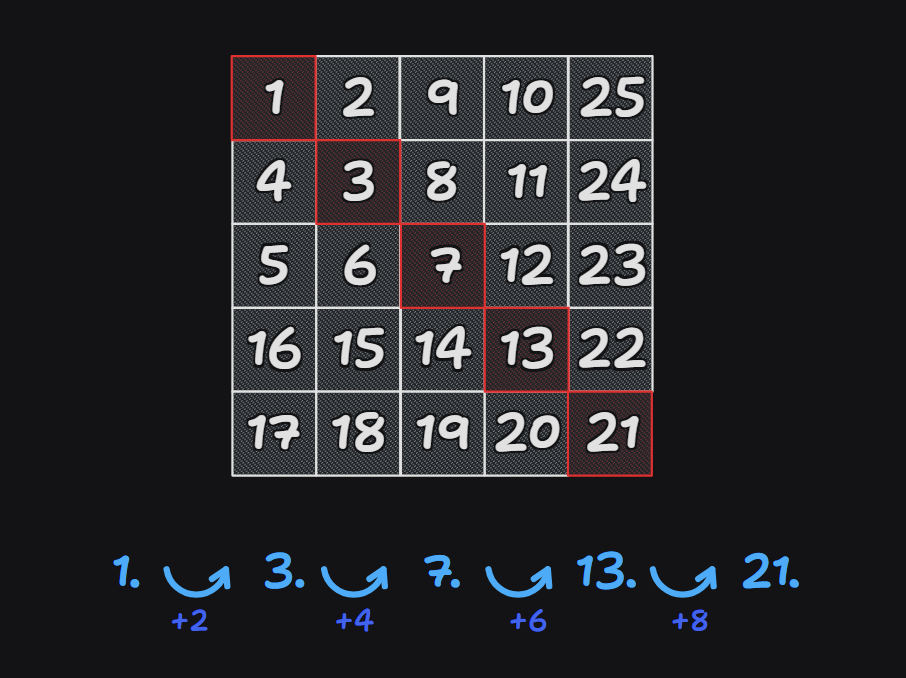
把圖畫得更大一點，就可以得到這樣的數列 $m_i$（OEIS: A002061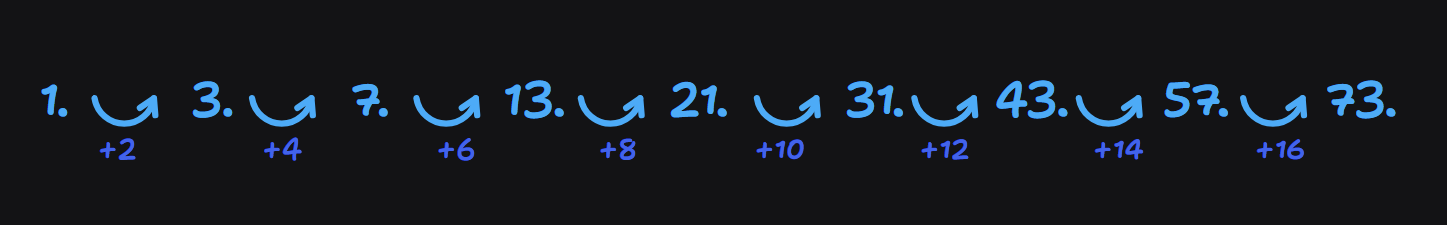）： 所以說，第 $\ell$ 層中對角線上格子的數字為 $N(\ell,\ell) = m_\ell = \ell \times (\ell - 1) + 1$。

這個數列又稱作 Hogben numbers。原始的出處比 CSES 的 number spiral 更像是一個螺旋：

接下來，看看其他格子之間的關係。

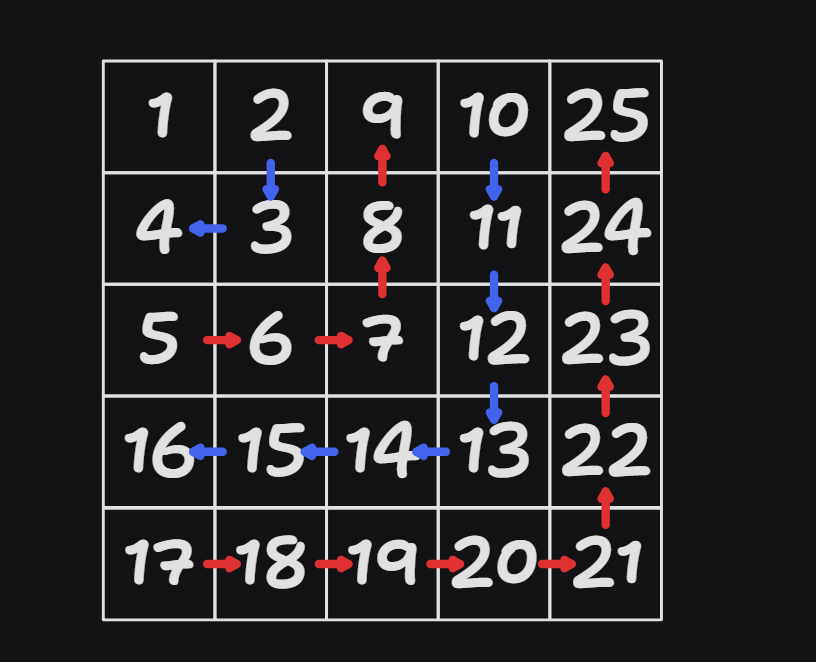
我們像上圖這樣一層層地看這些格子，我們說位於第 $y$ 橫列第 $x$ 直行的格子位在第 $\max(x, y)$ 層。那麼就會發現偶數層的數字都是由右上到左下增加，而奇數層則方向相反。

如此一來，要求出位在第 $y$ 橫列、第 $x$ 直行上的數字 $N(y,x)$ 是多少，我們可以根據它的層數以及它與同層的對角線格子之間的距離推導出來 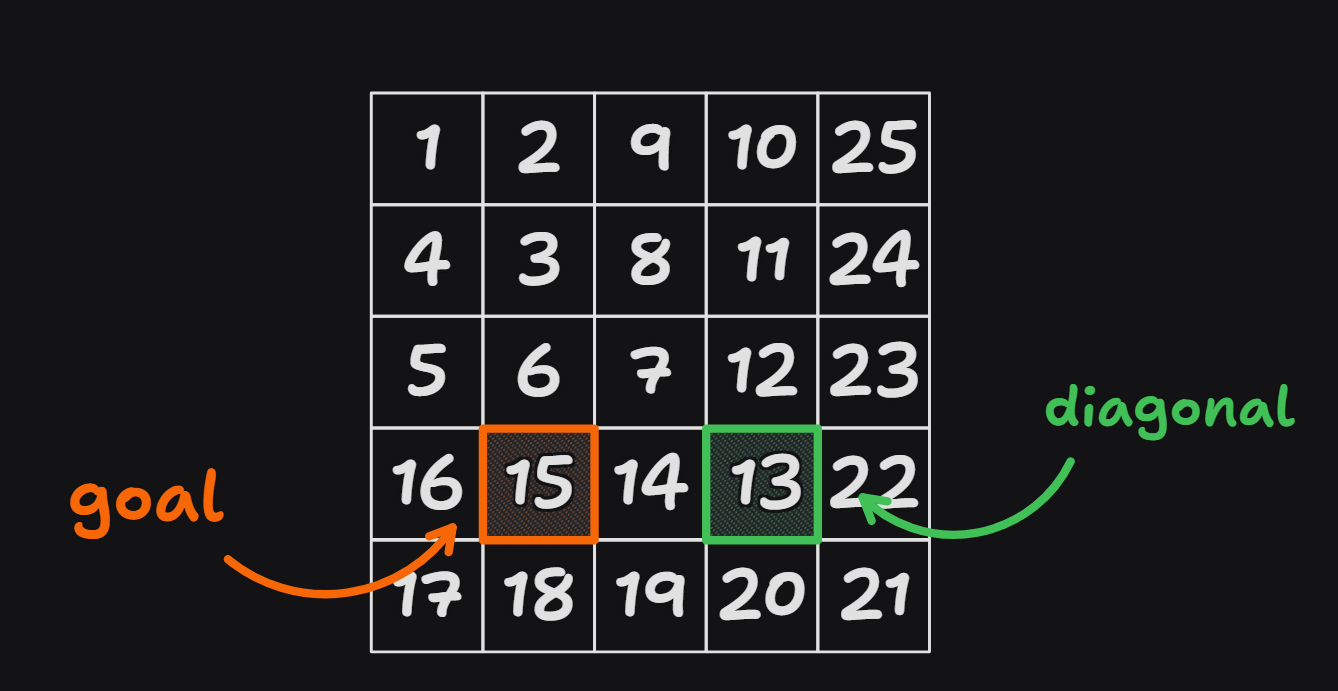比如說要求 $N(4,2)$ 是多少。首先可以算出它位在第 $4$ 層，並且位在對角線格子的左邊 $2$ 格。

因為數字 $N(4,2)$ 在第 $4$ 層，是偶數層，所以從對角線往左 $2$ 格到會讓數字增加 $2$。根據之前的結果知道對角線格子的數字是 $N(4,4) = m_4 = 4 \times 3 + 1 = 13$。那麼就能求出 $N(4,2) = 13 + 2 = 15$。

一般情況

我們令位於第 $y$ 橫列第 $x$ 直行的數字 $N(y,x)$ 坐落在第 $\ell$ 層，也就是說 $\ell = \max(x,y)$。 那麼根據它與同層對角線格子的相對位置我們有以下四種情形：

	$\ell$ 為奇數	$\ell$ 為偶數
在對角線左邊 $x < \ell$	$N(y,x) = m_\ell - (\ell - x)$	$N(y,x) = m_\ell + (\ell - x)$
在對角線上面 $\ell > y$	$N(y,x) = m_\ell + (\ell - y)$	$N(y,x) = m_\ell - (\ell - y)$

但按照定義，層數 $\ell = \max(x, y)$，表格內的 $\ell$ 根本可以用 $x$ 或 $y$ 代替。於是就變成下面這樣：

	$\ell$ 為奇數	$\ell$ 為偶數
在對角線左邊 $x < y$	$N(y,x) = m_\ell - (y - x)$	$N(y,x) = m_\ell + (y - x)$
在對角線上面 $x > y$	$N(y,x) = m_\ell + (x - y)$	$N(y,x) = m_\ell - (x - y)$

接著又因為減去一個數等於加上它的相反數，而且 $(x-y)$ 與 $(y-x)$ 互為相反數。所以說

• 當 $\ell$ 為奇數時，$N(y,x) = m_\ell + (x - y)$；
• 當 $\ell$ 為偶數時，$N(y,x) = m_\ell + (y - x)$。

注意事項

使用 C++ 要注意 int 在測資較大時會溢位。

範例程式碼

C++ 範例

#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(){
    ios::sync_with_stdio(0); 
    cin.tie(0); cout.tie(0);
    int t, x, y;
    cin >> t;
    while (t--) {
        cin >> y >> x;
        int lv = max(x, y);
        int m = lv * (lv-1) + 1;
        m += (lv % 2) ? x - y : y - x;
        cout << m << '\n';
    }
}